Abstract

Altitude, diameter and average slope of dome Milichius p.

Introduzione

I domi sono delle strutture sopraelevate presenti sulla superficie lunare formatesi a seguito della pressione esercitata dal magma proveniente dal sottosuolo lunare.

Queste particolari formazioni assumono una morfologia cupoliforme e talvolta presentano una depressione sommitale che si genera per effetto del collasso dell’apice del domo.

Normalmente si trovano in gruppi ma non è raro trovare dei domi isolati.

Il loro diametro non supera quasi mai 35 chilometri mentre presentano altezze di poche centinaia di metri pertanto si tratta di formazioni osservabili quando si trovano in prossimità del terminatore lunare.

Molti astrofili sono dediti all’osservazione dei domi poiché possono contribuite concretamente alla chiarificazione della loro natura e morfologia attraverso la misura dei parametri principali come altezza, diametro e pendenza media del domo.

Alcuni soci dell’Unione Astrofili Napoletani hanno compiuto queste misure su Milichius p.

Figura 1. Il domo Milichius p,indicato dai segmenti rossi, è contenuto nella mappa lunare N 57 della serie LAC.

Figura 2. La regione di Milichius ripresa dal Lunar Orbiter IV133H2

Si tratta di un domo presente nel quadrante nord-occidentale della Luna con coordinate Long W 31.20° – Lat N 10.08°. Il cratere Milichius, da cui il domo prende il nome, è facilmente identificabile tra i crateri Copernicus e Kepler.

Per la stima delle dimensioni del domo si è utilizzata un’immagine ottenuta il giorno 9 maggio 2014 alle ore 19:30 TU ( Figura 3).

Quest’ ultima è stata ripresa al fuoco diretto di un telescopio Schmidt Cassegrain con diametro dello specchio primario di 280 millimetri e lunghezza focale di 2800 millimetri. Per la ripresa è stata utilizzata una camera DMK con sensore CCD da 640×480 pixel quadrati da 5.6 micron di lato.

Figura 3. l’immagine utilizzata per la stima delle dimensioni del domo Milichius p ripresa al fuoco diretto del telescopio Schmidt Cassegrain da 11 pollici il giorno 9 maggio 2014 alle ore 19:30 TU

La scala dell’immagine

Per eseguire delle stime di dimensione su un’immagine CCD è necessario determinare la scala dell’immagine ovvero quanti metri sono sottesi da ciascun pixel del sensore.

Per quest’operazione si può procedere con vari metodi. Uno è quello di contare i pixel che compongono il diametro di un cratere di dimensioni note per poi procedere ad una semplice divisione. Questo metodo è molto immediato ma spesso i contorni del cratere non sono netti e definiti rendendo difficoltoso il conteggio dei pixel. Per questo motivo si è deciso di utilizzare alcune stelle doppie di separazione nota. Le stelle doppie essendo puntiformi consentono di contare con una maggiore precisione i pixel che le separano e quindi determinare la scala dell’immagine risulta più agevole.

		Osservatore “A”		Osservatore “B”
	separazione angolare in arcosec	pixel contati	scala immagine arc/pix	pixel contati	scala immagine arc/pix
Mizar	14,5″	33	0,439	33	0,439
Epsilon Lyrae	207,8″	485	0,428	484	0,429
Albireo	34,6″	83	0,417	85	0,407

Medie personali			0,428		0,425
Media tra i due osservatori	0,4265

Tabella 1. Stima della scala dell’immagine attraverso l’utilizzo delle stelle doppie

Come si osserva dalla Tabella 1 due osservatori ( osservatore A ed osservatore B ) hanno contato quanti pixel intercorrevano tra 3 coppie di stelle doppie ( Mizar, Epsilon Lyrae e Albireo). Dal rapporto tra separazione angolare e pixel contati si ottiene la scala dell’immagine. Ogni osservatore ha mediato la propria stima e per appiattire ulteriormente l’errore si è provveduto a mediare tra loro i risultati dei singoli osservatori ottenendo il valore finale di 0.4265 secondi d’arco per ogni pixel. Al momento della ripresa dell’immagine la Luna si trovava a 393060 chilometri. dalla Terra. A tale distanza l’angolo di 0.4265 secondi d’arco corrisponde a una lunghezza di 812 metri sulla superficie lunare.

Stima delle dimensioni del domo
L’altezza del domo (h) è il cateto di un triangolo rettangolo che ha come altro cateto la lunghezza dell’ombra proiettata dal domo (l) e come angolo (a) l’incidenza dei raggi solari sul domo.

Pertanto possiamo calcolare h con la formula:

h = l tan a (1)

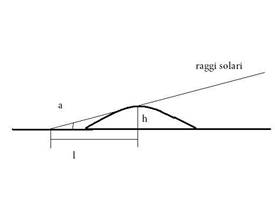Figura 4. L’altezza del domo (h) è il cateto minore del triangolo rettangolo che ha come cateto maggiore la lunghezza dell’ombra ( l )

Un ingrandimento dell’immagine (Figura 5) consente di stimare la lunghezza dell’ombra proiettata dal domo (l) e con l’aiuto di un software per fotoritocco si individua il valore di 6.5 pixel.

Ricordando che la scala dell’immagine è di 812metri/pixel si ottiene una lunghezza dell’ombra di 5278 metri.

Figura 5. L’ingrandimento dell’immagine consente una stima della lunghezza dell’ombra (l) e del diametro del domo (D) attraverso il conteggio dei pixel

Per determinare il valore dell’angolo a, che rappresenta l’inclinazione dei raggi solari sul domo, si è utilizzato il software Lunar Observer’s Toolkit che, tra le altre utilità, consente di individuare l’inclinazione dei raggi solari su qualsiasi punto della superficie lunare per un determinato istante.
Al momento della ripresa dell’immagine il Sole era alto su Milichius p 2.836°.
A questo punto si è potuta applicare la formula 1 che ci ha fornito un’altezza del domo di 261 metri rispetto al fondo circostante.
La figura 5 ci consente di stimare anche il diametro del domo (D) che risulta essere pari a 12 pixel
(9744 metri) come pure il diametro della depressione sommitale stimato in 2.5 pixel (2030 metri).

Conoscendo altezza e diametro del domo si può stimare la pendenza media (z) con la formula:

z = arctan(2h/D) (2)

Dall’applicazione della formula 2 si ottiene che Milichius p ha una pendenza media di 3.06°.

data ossevrazione	09-mag-14
ora TU	19.30
lunghezza ombra	5278 m
angolo incidenza raggi solari	2.836°
altezza domo	261 m
diametro domo	9744 m
pendenza media domo	3,06°
diametro depressione sommitale	2030 m

Tabella 2. di seguito sono schematizzati tutti i parametri misurati del domo Milichius p

Avendo a disposizione le misure è utile classificare il domo secondo la scala di Westfall (Tabella 3) che di basa su un’analisi di tipo morfologico.

Il domo Milichius p risulta essere di tipo DW2ag7j

Tipo
D	Domo
DC	Domo complesso

Fondo circostante
U	Altipiai
W	Mari
UW	Incerto

Pianta: asse maggiore
1	Meno di 5 km
2	Da 5 a 20 km
3	Da 20 a 35 km
4	Oltre 35 km

Forma
a	Circolare ( rapporto tra i due assi 1.00-1.25)
b	Ellittica ( rapporto tra i due assi 1.26-2,00)
c	Poligonale
d	Irregolare
e	Incerta

Profilo: pendenza media
5	Lieve ( inferiore a 2°)
6	Moderato ( da 2° a 5°)

Profilo: sezione
f	Semisferico
g	Sommità piatta
h	Sommità aguzza
i	Sommità multipla
f’	Semisferico asimmetrico
g’	Sommità piatta asimmetrico
h’	Sommità aguzza asimmetrico
i’	Sommità complessa

Dettagli superficiali: tipo
7	Depressione (cratere)
8	Elevazione
9	Fessura o valle
0	Assenti

Dettagli superficiali: posizione
j	Centrale
k	Asimmetrico
m	Marginale
n	Trasversale
p	Più dettagli

Tabella 3.Un estratto dello schema di classificazione dei domi lunari proposto da Westfall

Conclusioni
La misurazione delle ombre per la determinazione delle altezze relative è un metodo immediato e sufficientemente preciso per un’attività di tipo amatoriale.

Nel presente lavoro si è ipotizzato che il fondo circostante il domo fosse piatto e senza pendenze; quando così non è, la lunghezza dell’ombra viene deformata.

Inoltre una deformazione si registra anche nel caso in cui il domo si trova in prossimità del bordo lunare. Pertanto si può aumentare il livello di precisione nella misurazione correggendo queste distorsioni.

Bibliografia

[1] Lena R., Wohler C., Phillips J., Chiocchetta M.T., Lunar Domes, properties and formation processes, Springer, Chichester U.K., 2013.

[2] Marino A., Astronomia UAI, 2 (marzo aprile),15-19 (2008)

[3] www.lpi.usra.edu

[4] www.amlunsoc.org/lunar_dome_proj_.htm

[5] http://www.astropiombino.org/images/9/97/POF_10- 11_PROCEDURA_PER_IL_CALCOLO_DELLE_ALTEZZE_DELLE_MONTAGNE_LUNARI_.pdf

[6] Harry Jamieson’s, Lunar Observer’s Toolkit (LOT)